Twiddling
General Idea
Twiddling, sometimes referred to as Swizzling in Playstation communities, and better known as Morton Encoding or a Z/N-Ordered curve, is a method of data organization that retains Locality of Reference, which means that elements that reside physically close together in space, will be grouped together in memory. In the context of texture organization, this means that twiddling an image will make adjacent pixels to the right and below any given pixel reside close together in memory. This yields numerous benefits, such as easier calculation for AA and a texel configuration necessary for Vector Quantization compression.
Origins and Classical Implementation
The term "Twiddling" comes from the hacker term "bit-twiddling" owing to the classical way to calculate a Z-Ordered curve by manipulating the bits that make up the data (texel) index. The bit-twiddling way to arrive at a morton code is to take the binary representation of the X and Y coordinates of a texel and interleave them into one bitstring. The resultant bitstring will be twice the size of each individual input bitstring. For example, say you have a 4-bit number representing the X position of a Texel in a texture (e.g. XXXX) and you had a 4-bit number representing the Y position of a Texel (eg. YYYY), then your Z-Order position would be XYXY-XYXY (8-bit). This number is the index of where this texel lies in a new array that constitutes all the twiddled texels in the texture. If you convert every texel in the source texture into this new twiddled texture array, then iterating through the index will be the equivalent of navigating the source texture in a Z-pattern.
Whether one is a Z-ordered curve or an N-ordered curve depends on whether you shift the X or Y bitstring, effectively making the traversal width by height (Z) or height by width (N). Technically, the dreamcast uses an N-ordered curve.
Conceptualizing Twiddling
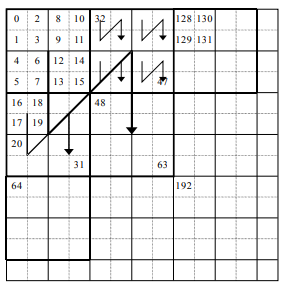
Lets start with a recap of what Twiddled textures even are. Twiddled textures is just a particular way of re-organising pixels in an image so they're quicker to render.
The example image where the numbers represent the original un-twiddled indexes and the "inverted Ns" show the original flow of indexes. Indexes from the original image were calculated from left to right, top to bottom (Scanline order). So we can see after index 0, number 1 is just below, 2 is to the right of 0 and 3 is just below 2. Then if we go to the next biggest inverted N we can see the order {0,1,2,3}, {4,5,6,7}, {8,9,10,11}, {12,13,14,15} following the same inverted N pattern.
So if we are given index i from an untwiddled image and wished to find the twiddled index, then its a process of recursively narrowing down what part of the twiddled image that pixel now lives in.
Protofall's Implementation
How to generated the twiddled index from an untwiddled texture
Lets start with a small example:
```
Original: Twiddled:
0 1 2 3 0 2 8 A 4 5 6 7 1 3 9 B 8 9 A B 4 6 C E C D E F 5 7 D F G H I J G I O Q K L M N H J P R O P Q R K M S U S T U V L N T V W X Y Z W Y % & ~ ! # $ X Z ^ * % ^ & * ~ # ( _ ( ) _ + ! $ ) +
```
The matching characters between the two images represent the same pixel, just relocated. These images would be 4 * 12 pixel images, but the steps work for any valid 2^x * 2^y sizes, where x and y are whole numbers.
Now lets say we want to find the twiddled index of the untwiddled "O" pixel (index 24). By hand we can work it out and tell the twiddle index should be "18", but what algorithm/logic can we use to find this automatically for any i?
Here are my steps:
- We first need to start by figuring out the "Biggest-Order Inverted-N" (BOIN) that fits in this image.
* Now if our starting image was a square, then the BOIN is the same size as the image * For rectangles like this, we have to find the smallest side first (width) then our BOIN is width * width
- If we start off with a rectangle, then we need to do an extra step that squares can skip.
* Notice how we can completely encapsulate the whole image with (bigger_side / smaller_side) == 3 BOINs? Our first step is to determine which of these BOINs our index i belongs in.
* We can take advantage of a quirk I mentioned earlier. Notice how the first BOIN contains the first 1/3 of the original pixels, the 2nd BOIN contains the next 1/3 and the 3rd BOIN contains the last 1/3.
* Therefore using the formula k = floor(i / (BOIN area == 4 * 4 = 16)) == 1 we can determine that our twiddled index is somewhere in the middle/2nd BOIN (Since k is of the set {0,1,2})
* Note the index where our BOIN starts according to the original texture. The first index in the 2nd BOIN is "16". Keep track of this value, lets call it d
* Also keep track of the index where our BOIN starts according to the twiddled texture, this is also 16 in this case. Lets add this to a running sum s
* Forget about the other two BOINs and subtract d from the indexes in our new BOIN as well as i
So now we have:
i == 8 0 2 8 A 1 3 9 B 4 6 C E 5 7 D F
Great! We can already see by hand that this still looks right, but how do we automatically solve square BOINs?
- In order to solve a square BOIN, we need to determine what quadrant our pixel is in
- So we determine how many pixels are in each quadrant (4 per quadrant here, == a), Then calculate k = floor(i / a) == 2 to know its in the 3rd quadrant (k is in the set {0,1,2,3}).
- That means its in the top right. So we need to set d = a * k), add our new s value to the running sum, discard the other quadrants, then subtract i and the new BOIN's indexes by d
* The easy way to calculate the new part of s is that:
* top left quadrant is 0
* top right quad is BOIN-width / 2
* bottom left is BOIN-width * (BOIN-height / 2)
* bottom right is (BOIN-width * (BOIN-height / 2)) + (BOIN-width / 2)
Now we have:
i == 0 0 2 1 3
You would repeat until we have a single pixel. Once we have the last pixel, our new twiddled index should be the running sum s (16 + 2 + 0 == 18)
Non-Dreamcast Bit-twiddling Hacks
A problem withe morton encoding is that it's an expensive operation normally unless attacked in the right way. It's usually far too costly to navigate a twiddled image every frame because it uses division and multiplication heavily. Thus there exists numerous bit-twiddling hacks to speed up this operation.
On modern x86_64 processors from Intel actually have instructions built in to handle z-ordered curves. These are the Parallel Bit Deposit (PDEP) and Parallel bit Extraction (PEXT) instructions, which can be used in conjunction to interleave a bitstring. But that's not useful for Dreamcast programming.
Another method for twiddling comes from multiplication without carry. A number multiplied upon itself using a carry-less multiplication will yield the original bitstring of the number interleaved with 0s. For example, given that the number 255 is 1111-1111 in binary, 255 multiplied without carry by 255 reveals a 16-bit number that is (1010-1010 1010-1010). Thus, if you use multiply without carry on the X and Y position of the texel in the texture, you'll arrive at two 16-bit numbers, e.g. X0X0-X0X0 X0X0-X0X0 Y0Y0-Y0Y0 Y0Y0-Y0Y0. If you bitshift the X value to the right by 1, and then OR the X bitstring by the Y bitstring, the resultant 16-bit bitstring will be twiddled.
However, the Dreamcast does not have a multiply-without-carry function, although you could create one that uses only addition like so:
``` int multiplyWithoutCarry(int a, int b) {
int result = 0; int multiplier = 1;
while (b != 0) {
int digit = b;
int temp = a;
while (digit > 9) {
digit -= 10;
temp += a;
}
while (digit > 0) {
result += temp;
digit--;
}
int divisor = 10;
int tempMultiplier = multiplier;
while (divisor > 1) {
if (divisor <= tempMultiplier) {
tempMultiplier -= divisor;
divisor = divisor << 1;
multiplier = multiplier << 1;
}
else {
divisor = divisor >> 1;
tempMultiplier = tempMultiplier >> 1;
}
}
b -= tempMultiplier; }
return result;
} ```
In this updated version, the /= 2 division operation has been replaced with bit shifting. The divisor and tempMultiplier variables are shifted left (<<) and right (>>) by 1 to perform the division or multiplication by 2.
Look-up Table Implementation
Taken from Stanford Bit-twiddling hacks page.
static const unsigned short MortonTable256[256] = {
0x0000, 0x0001, 0x0004, 0x0005, 0x0010, 0x0011, 0x0014, 0x0015, 0x0040, 0x0041, 0x0044, 0x0045, 0x0050, 0x0051, 0x0054, 0x0055, 0x0100, 0x0101, 0x0104, 0x0105, 0x0110, 0x0111, 0x0114, 0x0115, 0x0140, 0x0141, 0x0144, 0x0145, 0x0150, 0x0151, 0x0154, 0x0155, 0x0400, 0x0401, 0x0404, 0x0405, 0x0410, 0x0411, 0x0414, 0x0415, 0x0440, 0x0441, 0x0444, 0x0445, 0x0450, 0x0451, 0x0454, 0x0455, 0x0500, 0x0501, 0x0504, 0x0505, 0x0510, 0x0511, 0x0514, 0x0515, 0x0540, 0x0541, 0x0544, 0x0545, 0x0550, 0x0551, 0x0554, 0x0555, 0x1000, 0x1001, 0x1004, 0x1005, 0x1010, 0x1011, 0x1014, 0x1015, 0x1040, 0x1041, 0x1044, 0x1045, 0x1050, 0x1051, 0x1054, 0x1055, 0x1100, 0x1101, 0x1104, 0x1105, 0x1110, 0x1111, 0x1114, 0x1115, 0x1140, 0x1141, 0x1144, 0x1145, 0x1150, 0x1151, 0x1154, 0x1155, 0x1400, 0x1401, 0x1404, 0x1405, 0x1410, 0x1411, 0x1414, 0x1415, 0x1440, 0x1441, 0x1444, 0x1445, 0x1450, 0x1451, 0x1454, 0x1455, 0x1500, 0x1501, 0x1504, 0x1505, 0x1510, 0x1511, 0x1514, 0x1515, 0x1540, 0x1541, 0x1544, 0x1545, 0x1550, 0x1551, 0x1554, 0x1555, 0x4000, 0x4001, 0x4004, 0x4005, 0x4010, 0x4011, 0x4014, 0x4015, 0x4040, 0x4041, 0x4044, 0x4045, 0x4050, 0x4051, 0x4054, 0x4055, 0x4100, 0x4101, 0x4104, 0x4105, 0x4110, 0x4111, 0x4114, 0x4115, 0x4140, 0x4141, 0x4144, 0x4145, 0x4150, 0x4151, 0x4154, 0x4155, 0x4400, 0x4401, 0x4404, 0x4405, 0x4410, 0x4411, 0x4414, 0x4415, 0x4440, 0x4441, 0x4444, 0x4445, 0x4450, 0x4451, 0x4454, 0x4455, 0x4500, 0x4501, 0x4504, 0x4505, 0x4510, 0x4511, 0x4514, 0x4515, 0x4540, 0x4541, 0x4544, 0x4545, 0x4550, 0x4551, 0x4554, 0x4555, 0x5000, 0x5001, 0x5004, 0x5005, 0x5010, 0x5011, 0x5014, 0x5015, 0x5040, 0x5041, 0x5044, 0x5045, 0x5050, 0x5051, 0x5054, 0x5055, 0x5100, 0x5101, 0x5104, 0x5105, 0x5110, 0x5111, 0x5114, 0x5115, 0x5140, 0x5141, 0x5144, 0x5145, 0x5150, 0x5151, 0x5154, 0x5155, 0x5400, 0x5401, 0x5404, 0x5405, 0x5410, 0x5411, 0x5414, 0x5415, 0x5440, 0x5441, 0x5444, 0x5445, 0x5450, 0x5451, 0x5454, 0x5455, 0x5500, 0x5501, 0x5504, 0x5505, 0x5510, 0x5511, 0x5514, 0x5515, 0x5540, 0x5541, 0x5544, 0x5545, 0x5550, 0x5551, 0x5554, 0x5555
};
unsigned short x; // Interleave bits of x and y, so that all of the
unsigned short y; // bits of x are in the even positions and y in the odd;
unsigned int z; // z gets the resulting 32-bit Morton Number.
z = MortonTable256[y >> 8] << 17 |
MortonTable256[x >> 8] << 16 |
MortonTable256[y & 0xFF] << 1 |
MortonTable256[x & 0xFF];
For more speed, use an additional table with values that are MortonTable256 pre-shifted one bit to the left. This second table could then be used for the y lookups, thus reducing the operations by two, but almost doubling the memory required. Extending this same idea, four tables could be used, with two of them pre-shifted by 16 to the left of the previous two, so that we would only need 11 operations total.
Binary Magic Numbers Implementation
Taken from Stanford Bit-twiddling hacks page.
[code]
static const unsigned int B[] = {0x55555555, 0x33333333, 0x0F0F0F0F, 0x00FF00FF};
static const unsigned int S[] = {1, 2, 4, 8};
unsigned int x; // Interleave lower 16 bits of x and y, so the bits of x
unsigned int y; // are in the even positions and bits from y in the odd;
unsigned int z; // z gets the resulting 32-bit Morton Number. x and y must initially be less than 65536.
x = (x | (x << S[3])) & B[3];
x = (x | (x << S[2])) & B[2];
x = (x | (x << S[1])) & B[1];
x = (x | (x << S[0])) & B[0];
y = (y | (y << S[3])) & B[3];
y = (y | (y << S[2])) & B[2];
y = (y | (y << S[1])) & B[1];
y = (y | (y << S[0])) & B[0];
z = x | (y << 1);
[/code]
DISCLAIMER
This theorized solution has only been tested on a few examples by hand, so I might have missed something. But I believe at least the general logic of this is sound. Also note for implementation, some of the divisions could be replaced with bit-shifting since some of those numbers are guaranteed to be powers of 2.
For an example of an algorithm that does the reverse (Convert twiddled index to untwiddled), you can refer to this code made by JamoHTP