Twiddling

General Idea

Twiddling, sometimes referred to as Swizzling in Playstation communities, and better known as Morton Encoding or a Z/N-Axised curve, is a method of data organization that retains Locality of Reference, which means that elements that reside physically close together in space, will be grouped together in memory. In the context of texture organization, this means that twiddling an image will make adjacent pixels to the right and below any given pixel reside close together in memory. This yields numerous benefits, such as easier calculation for AA and a texel configuration necessary for Vector Quantization compression.

The term "Twiddling" comes from the hacker term "bit-twiddling" owing to the classical way to calculate a Z-Ordered curve by manipulating the bits that make up the texel index.

Conceptualizing Twiddling

Lets start with a recap of what Twiddled textures even are. Twiddled textures is just a particular way of re-organising pixels in an image so they're quicker to render.

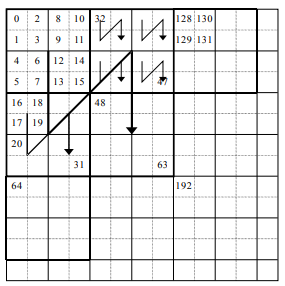
The example image where the numbers represent the original un-twiddled indexes and the "inverted Ns" show the original flow of indexes. Indexes from the original image were calculated from left to right, top to bottom (Scanline order). So we can see after index 0, number 1 is just below, 2 is to the right of 0 and 3 is just below 2. Then if we go to the next biggest inverted N we can see the order {0,1,2,3}, {4,5,6,7}, {8,9,10,11}, {12,13,14,15} following the same inverted N pattern.

So if we are given index i from an untwiddled image and wished to find the twiddled index, then its a process of recursively narrowing down what part of the twiddled image that pixel now lives in.

Dreamcast Implementation

How to generated the twiddled index from an untwiddled texture

Lets start with a small example:

```

Original: Twiddled:

0 1 2 3 0 2 8 A 4 5 6 7 1 3 9 B 8 9 A B 4 6 C E C D E F 5 7 D F G H I J G I O Q K L M N H J P R O P Q R K M S U S T U V L N T V W X Y Z W Y % & ~ ! # $ X Z ^ * % ^ & * ~ # ( _ ( ) _ +  ! $ ) +

```

The matching characters between the two images represent the same pixel, just relocated. These images would be 4 * 12 pixel images, but the steps work for any valid 2^x * 2^y sizes, where x and y are whole numbers.

Now lets say we want to find the twiddled index of the untwiddled "O" pixel (index 24). By hand we can work it out and tell the twiddle index should be "18", but what algorithm/logic can we use to find this automatically for any i?

Here are my steps:

• We first need to start by figuring out the "Biggest-Order Inverted-N" (BOIN) that fits in this image.

   * Now if our starting image was a square, then the BOIN is the same size as the image
   * For rectangles like this, we have to find the smallest side first (width) then our BOIN is width * width

• If we start off with a rectangle, then we need to do an extra step that squares can skip.

   * Notice how we can completely encapsulate the whole image with (bigger_side / smaller_side) == 3 BOINs? Our first step is to determine which of these BOINs our index i belongs in.
   * We can take advantage of a quirk I mentioned earlier. Notice how the first BOIN contains the first 1/3 of the original pixels, the 2nd BOIN contains the next 1/3 and the 3rd BOIN contains the last 1/3.
   * Therefore using the formula k = floor(i / (BOIN area == 4 * 4 = 16)) == 1 we can determine that our twiddled index is somewhere in the middle/2nd BOIN (Since k is of the set {0,1,2})
   * Note the index where our BOIN starts according to the original texture. The first index in the 2nd BOIN is "16". Keep track of this value, lets call it d
   * Also keep track of the index where our BOIN starts according to the twiddled texture, this is also 16 in this case. Lets add this to a running sum s
   * Forget about the other two BOINs and subtract d from the indexes in our new BOIN as well as i

So now we have:

---

i == 8 0 2 8 A 1 3 9 B 4 6 C E 5 7 D F

---

Great! We can already see by hand that this still looks right, but how do we automatically solve square BOINs?

• In order to solve a square BOIN, we need to determine what quadrant our pixel is in
• So we determine how many pixels are in each quadrant (4 per quadrant here, == a), Then calculate k = floor(i / a) == 2 to know its in the 3rd quadrant (k is in the set {0,1,2,3}).
• That means its in the top right. So we need to set d = a * k), add our new s value to the running sum, discard the other quadrants, then subtract i and the new BOIN's indexes by d

   * The easy way to calculate the new part of s is that:
       * top left quadrant is 0
       * top right quad is BOIN-width / 2
       * bottom left is BOIN-width * (BOIN-height / 2)
       * bottom right is (BOIN-width * (BOIN-height / 2)) + (BOIN-width / 2)

Now we have:

---

i == 0 0 2 1 3

---

You would repeat until we have a single pixel. Once we have the last pixel, our new twiddled index should be the running sum s (16 + 2 + 0 == 18)

DISCLAIMER

This theorized solution has only been tested on a few examples by hand, so I might have missed something. But I believe at least the general logic of this is sound. Also note for implementation, some of the divisions could be replaced with bit-shifting since some of those numbers are guaranteed to be powers of 2.

For an example of an algorithm that does the reverse (Convert twiddled index to untwiddled), you can refer to this code made by JamoHTP